贝塞尔曲线(Bezier curves)是曲率的一种典型代表,而且在很多应用中都会运用到,比如计算机的图形学中、字体和动画。如果你以前玩过CSS,那么你可能就运到过贝塞尔曲线。例如,在CSS的时间函数(timing function)中就有一个贝塞尔曲线——x轴和y轴的距离用来确定时间。
为什么要使用它们
从自己的角度来说,我们需要画一条曲线,它可以会消耗100px。画这样的一条曲线是非常的方便。不幸运的是,画这样的曲线会有非常多的原因,最明显的就是存储的开销非常的大。
如果我们可以调用一个函数100次,而且每次收集一个点。为了这个目标,我们可以创建一个函数:
/**
* @param {Number} t Number from 0 to 1.
* @return {Array} Point on the curve
*/
function getCurveLocation(t) { ... }
函数需要一个从0到1的数字,这主要是我们需要画100个点,我们把这个函数称之为getCurveLocation,它的值空间将是100次。
var points = []
for(var i = 0; i <= 100; i++) {
points.push(getCurveLocation(i * .01))
}
我们都完成了,这个设置代表我们的曲线在任意的像素位置。这个很简单——我们只是增加和减少循环计数从而得到所需要的像素数量,然后再渲染到屏幕上。
定义
getCurveLocation是如何定义的呢?那是贝塞尔曲线发挥作用的地方。它的定义一般如下:
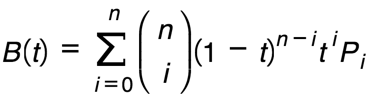
让我们来分解这个公式。这一开始只是一个实现一个方式。就算你不理解这个公式的每一个部分,这并不重要,稍后我们会通过示例将这一切联系在一起。
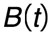
B是一个函数,它接收一个数字的参数t,而且它的值是从0到1,并且其返回的是曲线上的每个点。

n代表贝塞尔曲线的程度,其角度越高,曲线形状就越复杂。大多数的时候,二次平方和三次立方是我们所需要的。i是一个整数,从0开始,并且每个循环将增加一次。
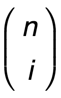
代表二项式系数。如果我们扩展出二次项,比如(x+y)^n。我们这可以走一个捷径。不管是不是二次项,比如n=3和i=2,都可以快速通过这个组合快速的评估这个表达式。

代表一个多项式中的特定项。PI是其中的一个控制点。
知识点
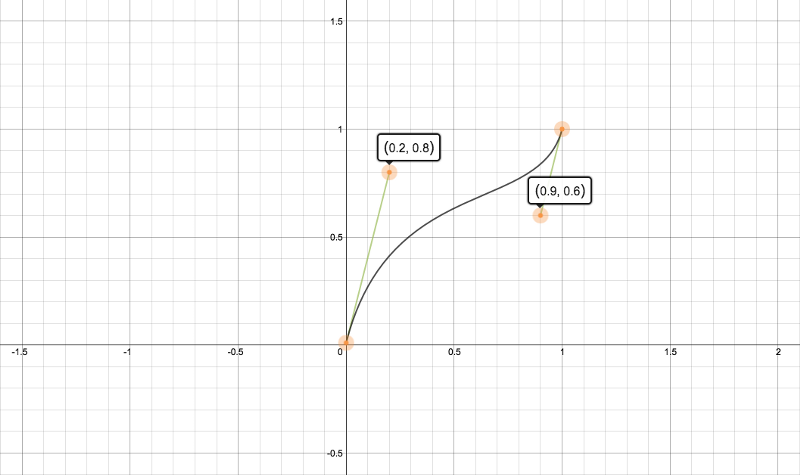
从下面的向个示例开始,让我们创建一个贝塞尔曲线:
P0 = (0,0)
P1 = (.2, .8)
P2 = (.9, .6)
P3 = (1, 1)
因为这有4个点,而这个贝塞尔曲线有三个点,而它有四个循环点,而且每个循环点的结果如下:

循环1:

循环2:
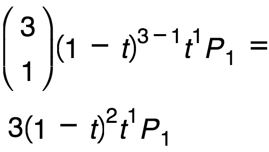
循环3:

循环4:

最后的多项式:
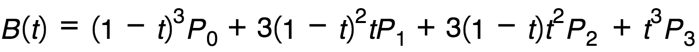
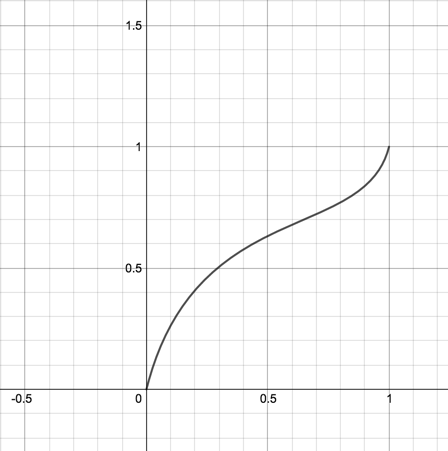
让欠通过P的变量来绘制其对应的方程式:
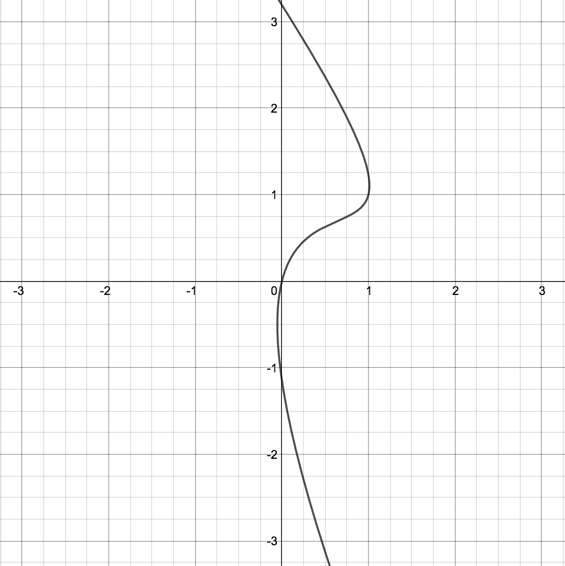
你可以觉得这条曲线不太有用,但这个从0到1的域是非常有意义的:
看起来应该蛮熟悉的,它是文章开始使用的贝塞尔曲线。从0至1之间的域是非常重要的,因为所有有趣的事情都发生在这两个值上面。先来看看t=0时的多项式:

接下来再看看t=1的多项式:
我们得到了最后一个点。不管第一个点和最后一个点在哪里,t=0将始终返回第一个点,t=1将始终返回最后一个点。这点真的非常的强大,不管多项式有多复杂,都可以很容易的分析路径的开始点和结束点。任何其他的t值不会取消。例如,在这里可以改变P1这个第二点,得到不同的曲线咱径:
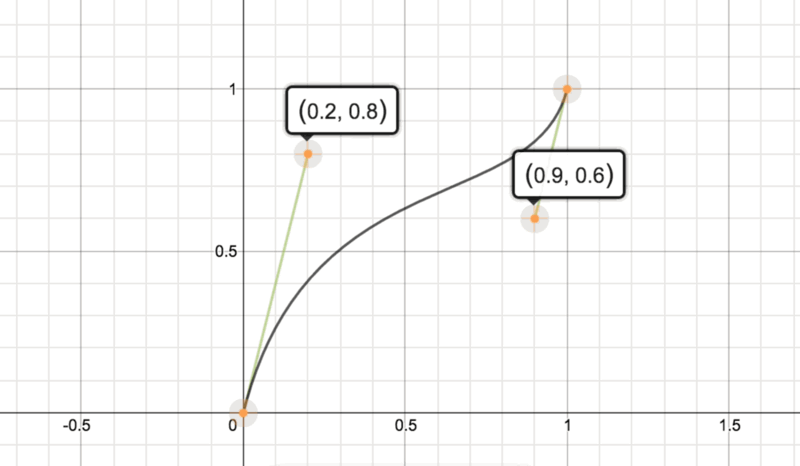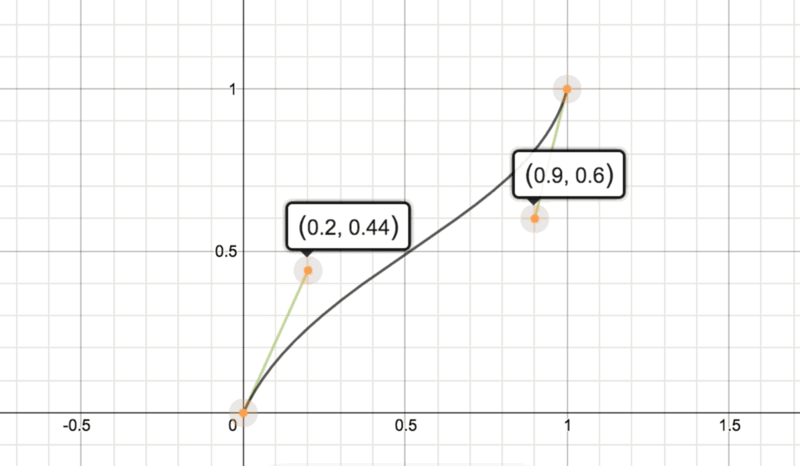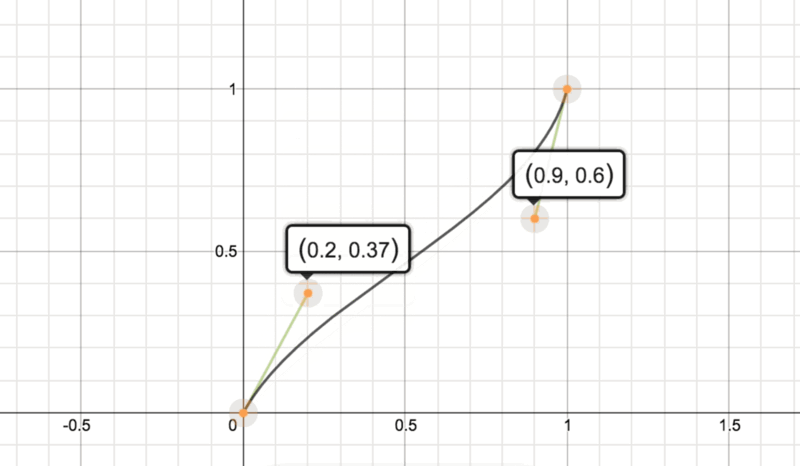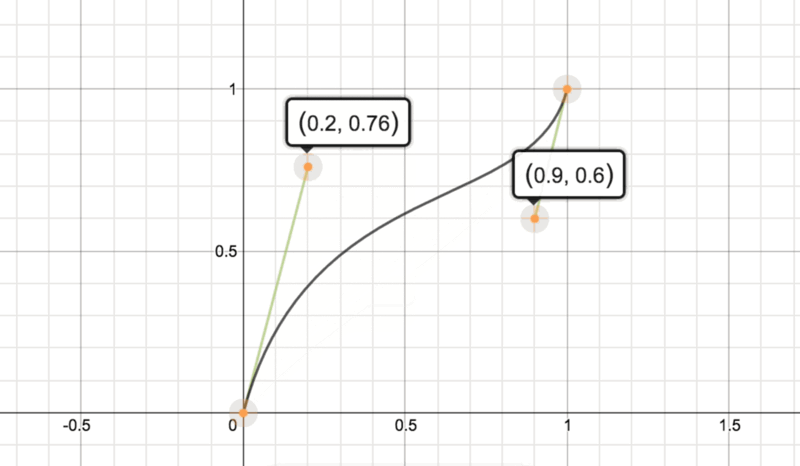
当P1增加时,曲线向上弯曲,然而它的速度越来越慢。可以修改P1的值来证明这一点。而且我们可以通过公式来阐述这一切。
让我们来看看t=.25时曲线的弯曲程度:

显而易见,P1比P2更有发言权。现在我们来看看t=.75的效果:

现在P2更高,实现逆转。所以当t每增加一次,那么其会有一个独特的控制点。
在文中使用了三次贝塞尔曲线作为示例,直觉上也适用于其他的贝塞尔曲线。例如,贝塞尔曲线有三个点,两点终端生个控制点:

曲线会根据控制点P1做变化。随着P1和端端在同一直线上时,会得到一条直线。这也就是得到我们常见的linear效果。这一现象非常值得我们去探索。同时希望你能通过这篇文章得到一些洞察力。从一个简单的输入0到1可以得到对应的曲线。
扩展阅读
本文根据@Shawn O'Mara的《Mathematical Intuition Behind Bezier Curves》所译,整个译文带有我们自己的理解与思想,如果译得不好或有不对之处还请同行朋友指点。如需转载此译文,需注明英文出处:https://buildingvts.com/mathematical-intuition-behind-bezier-curves-2ea4e9645681#.k6pdvyhgc。
如需转载,烦请注明出处:http://www.w3cplus.com/animation/mathematical-intuition-behind-bezier-curves.html
