这篇文章的思路以及文章中所涉及到的数学公式都来自于@Thai Pangsakulyanont分享的《Spring Animation in CSS》一文。
CSS Animation在Web Animation中已不是新技术,不过在制作动画的时候,或许常常纠结timing-function如何使用。一般情况之下,都会使用animation-timing-function/transition-timing-function自带的几个关键词动画函数。稍为熟悉Web Animation的同学可能会使用cubic-bezier.com帮助自己创建一些timing-function。往往这一切都只是局限于使用,而不知道其原理究竟是什么。
另外,使用这些基本的timing-function几乎是无法模拟出一个真实弹跳(类似弹簧弹性)的动画效果。
其实,事实并不是如此。为什么这么说呢?在制作动画过程中,数学可能帮我们做很多更有意义的事情,比如说借助数学微积分的一些原理就可以让我们制作出更真实的动画效果。就比如说弹簧弹跳动效。那么这篇文章讲的就是这样的内容,如果你感兴趣欢迎继续往下阅读。
首先来看一个动画效果的示例:
话说这些数学公式都是来自于@Thai Pangsakulyanont分享的《Spring Animation in CSS》一文。而且自己离开学校有近二十年,很多知识都还给了老师,如果文章有不对之处,还请大家多多指正。
为什么选择CSS Animation
这是一个亘古不变的话题,其实没有啥好纠结的。对于一位在JavaScript方面啥都不懂的同学而言,他往往追过的是如何将动画效果能通过CSS完成,而且达到近似JavaScript方面的效果(虽然这几乎是不太可能,但往往很多时候是不会相关很远)。那么抛开这些而言,我们从技术角度出发,目前实现Web Animation有很多优秀的库,比如React-motion、Velocity.js和GSAP。但它们都有一个问题:JavaScript访问DOM都是单线程。而使用CSS Animation没有这一问题存在。
Tweening的基础知识
来看一个简单的动画,比如将一个盒子从left:100px推到left:200px。
这意味着,随着时间的推移,在100px至200px之间不要停。
当动画执行时,我希望覆盖的面是减小100px(从100%到0%),与此同时,覆盖的而增加到200px(从0%到100%)。
处理动画到200px有一个过程,我们把这个过程简称为p,通过p使用使用下面的公式,可以计算出每个时间段left的值:
$$left: (1-p)(100px)+p(200px)$$
下面这张图解释了它是如何工作的:
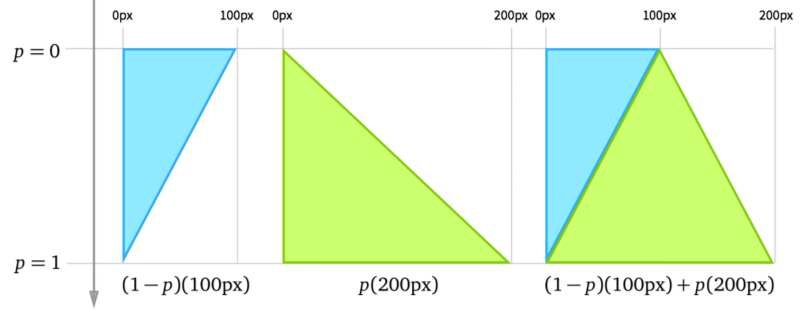
来概括一下,如果动画要从A过渡到B,而运动进展是p,那么他的属性值将是:
$$(1-p)A+pB$$
有些同学可能喜欢写成这样:
$$A+p(B-A)$$
把这个称之为lerp或者linear interpolation(线性插值)。
虽然把这个称为线性,但现实世界的动画并不是线性的。例如,你可能希望动画开始是缓慢的,而快要结束时速度是快速的(相当于物体做加速度)。在动画播放中可以使用一个缓动函数(easing function),但这样处理过程和时间就不是线性操作。
而缓动函数主要是用来创建时间和动画发展之间的关系。
缓动函数指定动画效果在执行时的速度,使其看起来更加真实。现实物体照着一定节奏移动,并不是一开始就移动很快的。当我们打开抽屉时,首先会让它加速,然后慢下来。当某个东西往下掉时,首先是越掉越快,撞到地上后回弹,最终才又碰触地板。——easing function
注:mj.js官网对easing function做了很详细的阐述。
物理(Physics)
下面一个弹簧块,假设在它不动的时候位置是x = 1:
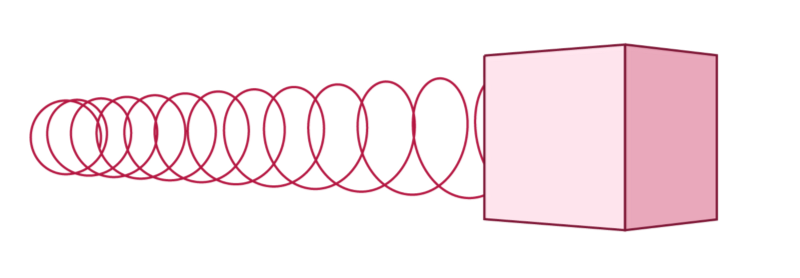
现在你推了一下弹簧,它的位置为成了x = 0:

当你松开手,不推弹簧时,弹簧就会来回的移动,直到弹簧到达平衡位置x = 1,才会停下来不动。
这就像easing function。也就是说它是一个时间函数(timing-function),这个时间函数是从0%开始到100%结束。而弹簧是这里面的物体之一。
下面的内容开始复杂起来了,顺间感觉我们不是在说CSS Animation的事情,而是开始在学习物理了,而且下面还会涉及到一些物理方程式(力学、弹簧相关物理方程式)。
首先来看Spring Force拉着弹簧块回到平衡位置。这里的X是物体的位移的平衡位置:
$$F_{s}=-kX$$
还有就是damping force减缓运动的阻力。想像一下,要是没有这个阻力,弹簧来回摆动能停下来?
$$F_{d}=-cv$$
那么这样就可以计算出用在弹簧上的力有多大:
$$F=F_{s}+F_{d}=-kX-cv$$
想必大家都听过牛顿第二定律吧:
$$F=ma$$
为了简单起见,我们假设mass(要是没有记错,这个好像是指物体的密度一样)值为1(即m=1),这样就可以得到:
$$F=-kX-cv$$ $$ma=-kX-cv$$ $$a=-kX-cv$$
现次,X代表物体从其平衡位置开始移动。这就意味着,如果我们想从x = x到x = 1,那么我们要每次移动x-1才能到达那个指定位置。
$$X=x-1$$
这样可以计算出left的值:
$$a=-k(x-1)-cv$$
这就是我们的运动方程式。现在我们完成了从物理方程式中得到了需要的运动方程式。
计算
如果你还记得微积分的一些知识,那么下面的内容对你来说不是难事。接下来使用微积分一些公式来计算出物体运动的位置和时间的关系。
$$x=f(t)$$
根据位置,算出速度:
$$v=\frac{dx}{dt}=f'(t)$$
根据速度,得到加速度:
$$a=\frac{dv}{dt}=f''(t)$$
回忆一下运动的方程式:
$$a=-k(x-1)-cv$$
使用上面的公式来替代x、v和a,现在你看到的公式是这样的:
$$f''(t)=-k(f(t)-1)-cf'(t)$$
这是一个微分方程式。这些对于我来说太复杂了,如果你和我一样不知道如何使用自己所掌握的微积分知识来解决,那么可以使用Wolfram | Alpha帮你。
为了能让事情变得简单一些,我们来做一些限制,减少其中的复杂难度。
记住,我们让块移动之前,块的位置假设在x=0。也就是说块的初始位置是x=0,初始时间是t=0,这样得到:
$$f(0)=0$$
我们也知道,特体在放手前它是不会移动的,这也意味着,咱们还有这样的一个公式:
$$f'(0)=0$$
不幸的是,Wolfram | Alpha使用k和c这样的变量无法解这个方程式,所以我们还需要一些其他的值。
比如react-motion库中的wobble动画,设置了k=180,c=12。这样就可以解方程式:
$$f(0)=0$$ $$f'(0)=0$$ $$f''(t)=-180(f(t)-1)-12f'(t)$$
在Wolfram | Alpha中输入:
f(0) = 0; f'(0) = 0; f''(t) = -180(f(t) - 1) - 12f'(t)
你可以看到下图:
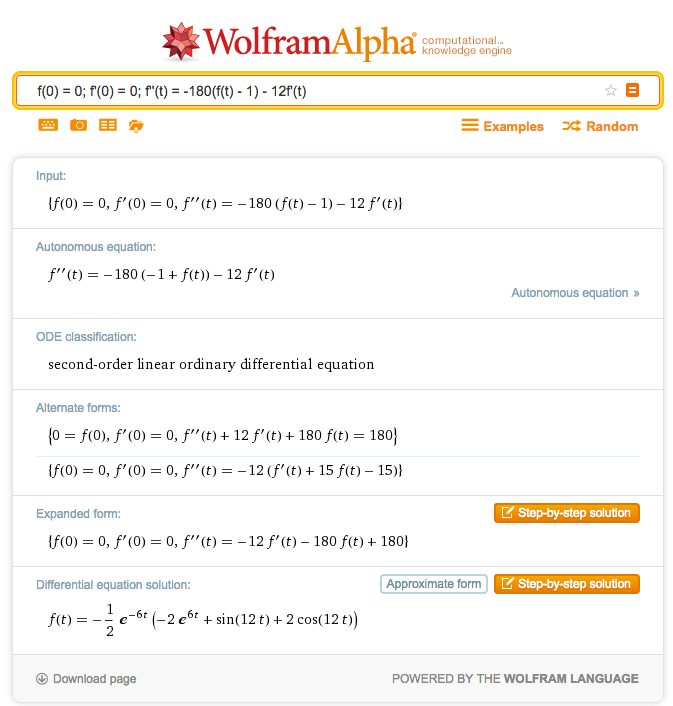
Wolfram | Alpha给我们的答案是:
$$x=-\frac{1}{2}e^{-6t}(-2e^{6t}+sin(12t)+2cos(12t))$$
哪里来的½, 6, sin()和 cos()?我也不知道,这对于我来说太复杂,太难,太不可思议。
但它看上去是合法的(合不合法,我也看不懂,暂当Wolfram | Alpha计算不会出错),因为sin和cos感觉是在做一个摆动运动,就像弹簧一样。把t=0到t=1按每0.01为分隔值,绘制出一张像下面的图:

CSS Animation
我们不能把这么复杂的方程式运用到CSS,但我们可以生成一些近似方程式的。在CSS Animation中可以通过@keyframes来指定,但是我们的方程是一个连续函数。
正如上面绘制的图一样,我们把这个运用到CSS的@keyframes中,例如,动画持续的时间为1s,那么CSS代码看起来像这样:
@keyframes keyframe-name {
0% { /* css code for t=0.00s */ }
1% { /* css code for t=0.01s */ }
2% { /* css code for t=0.02s */ }
3% { /* css code for t=0.03s */ }
/* ... */
99% { /* css code for t=0.99s */ }
100% { /* css code for t=1.00s */ }
}
这样写起来,你肯定要骂娘了,也切实际。不过可以使用一些CSS预处理器来生成。下在我们使用Sass来做。
@Thai Pangsakulyanont分享的《Spring Animation in CSS》一文使用的是Stylus。由于自己对Stylus不太熟悉,将其换成Sass。
首先要使用Sass把Wolfram | Alpha给我们的答案换成一个函数:
@function spring-wobbly($t) {
@return -0.5 * pow(2.71828, (-6 * $t)) * (-2 * pow(2.71828, (6 * $t)) + sin(12 * $t) + 2 * cos(12 * $t))
}
由于Sass自身不提供这些数学函数,比如sin()和cos()之类。如果这些函数都要自己去写是非常的蛋疼,这里给大家推荐一个非常优秀的Sass库MathSass。这个库涵盖了常见的函数。详细的使用,可以阅读其使用规范。
比如,在上面的函数前引入math:
@import "node_modules/mathsass/dist/math";
实际项目中把上面的地址换成你自己的项目地址才能有效。
还记得前面使用插值函数覆盖tweeing动画那部分吗,我们也可以写一个函数:
@function lerp($a, $b, $p) {
@return $a + $p * ($b - $a);
}
接下来生成@keyframes:
@keyframes move {
@for $i from 0 through 100 {
#{$i}% {
left: lerp(100px, 200px, spring-wobbly($i / 100));
}
}
}
生成的CSS:
接下来只需要引用声明好的动画:
.box {
animation: 1s move linear;
animation-fill-mode: both;
}
效果如下:
在动画中其实运用到数学原理还是很多的,比如@bboy90的《CSS3动画帧数科学计算法》一文详细介绍了如何通过公式合理的计算@keyframes。另外附上@月影 姐姐分享的PPT,里面详细介绍了一些动画控制:
上面PPT里的数学公式和一些DEMO,非常值得我们去思考。另外附上一个视频:
定制
回到文中主要介绍的内容,在实际动画制作中,你完全可以根据自己需要的材质密度和摩擦系数去自定义自己所需的动画效果。
当然你也可以尝试去修改f'(0)的值。比如设置一个负值,让盒子从相反的方向反弹回来。
你也可以使用不同的参数,让他运动得更快或更慢。总而言之,你可以根据上面的原理,去制定所需要的一切动画效果。
总结
谁说编程不需要数学,今天不是编程,仅仅只是做一个动画效果,都运用到了物理学和数学中的微积分。所以说,你学的一切都是有用的。
在我看来,不管你懂不懂微积分,或者说物理相关的知识,你只需要知道其中的原理,哪怕你都不懂这些,你也可以借助第三方工具(比如说文中提到的Wolfram Alpha)可以帮助你解决你所欠缺的知识。
总而言之,学到的都是属于你的。如果想让一件事情做得更为完美,那么你的知识都将是其中的基石。
本文思路来源于自于@Thai Pangsakulyanont分享的《Spring Animation in CSS》一文。对原文做过一些修改,您可以直接阅读原文。
如需转载,烦请注明出处:http://www.w3cplus.com/animation/spring-animation-in-css.html
